“Let me Unsee” by Asbestos, Belfast, August 2023.
The T in GPT
In all the excitement around OpenAI’s ChatGPT two things are often not mentioned:
-
the underlying architecture of Generative Pre-trained Transformer (GPT) models, the Transformer, was invented and made public by Google
-
despite these models’ impressive capabilities, and their scale and complexity, the underlying mathematics involved (at least in terms of the components used) is relatively simple
As these models are increasingly important it felt worth learning more about them. This is the first in a series of notes to help me understand the area better. It covers Attention, the key mechanism at the heart of how Transformers work. If you have any comments on it please let me know.
The neural networks in Large Language Models (LLMs) have billions of weights. They are initially trained using text from much of the public internet by adjusting the weights to improve their performance predicting the next word from the text input. In LLMs that have a transformer architecture, such as a GPT, are multiple layers of weights based on the attention mechanism. Although exactly why this architecture works is not fully understood, it is generally accepted that it allows the models to build up a rich mathematical representation of words, the relationships between them and of language itself. Enabling them, with some further training, to ‘understand’ questions and answer them.
What follows implicitly assumes some knowledge of vectors, matrices and how
neural networks work. The linear algebra involved is though pretty minimal.
The main thing used without explanation is that if we have an n dimensional vector v and want to
transform it into an m dimensional vector v*, then we need to multiply it by
a matrix with dimensions m x n (where m is the number of rows and n the
number of columns) i.e. v*=Mv.
1. Encoding and embedding (converting words into vectors)
The text that the model is trained on is split up into separate blocks of text, such as paragraphs and sentences. In order to feed this text into a neural network we take these blocks and split them into tokens which are the components that the text is made of. These tokens can be words and for simplicity I’ll call them that, but they can also be parts of speech. The tokens are encoded into numbers to keep track of them e.g. the word ‘cat’ might be given the number 240, the word ‘dog’ 241 etc. These numbers are converted into vectors representing the words, one vector per word, using a technique called embedding. In an embedding words with a similar meaning have vectors that are closer together. An embedding vector can be 1000s of numbers long in some of the larger GPT models, but would more commonly in the hundreds for embeddings run on a normal computer. We can represent text as a series of vectors, which we process in the Transformer using attention.
Embeddings are created roughly speaking as follows. In the simplest kind of embedding we have a neural network which consists of a matrix of weights of dimensions (dimension of the embedding we want x the number of distinct tokens/words in all the text i.e. the vocabulary it is written in). The embedding dimension is typically a lot smaller than the vocabulary size. Here we’ll take the model’s embedding dimension to be 300.
We then have another matrix of weights that goes from the embedding dimension back to the number of distinct tokens/words and then a layer which from that outputs a probability of an individual word. This layer has the functional form below and is known as a softmax. It takes a set of n inputs (xi, where i = 1 to n. n being the number of distinct words in all the text analysed) and produces n outputs that sum to 1 i.e. it gives a probability distribution.
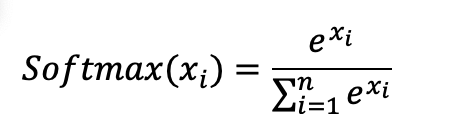
We then input pieces of text into the network as a series of vectors. The vectors have the dimension of the number of different words used in all of the input texts. Their values are 1 for the index corresponding to a given word’s allocated number and 0 everywhere else (a so-called One Hot Encoding). For example if there were 15,000 different words used in all the texts, these vectors would have 15,000 elements (have a 15,000 dimensionality). If the word dog was allocated the number 241 the corresponding vector would be 1 for its 241’th element and the rest of the 15,000 elements would be 0.
The vectors representing words in pieces of text are fed into the network and multiplied by the matrices of weights before outputting the probability distribution of different words. There are different ways to generate embeddings, but a standard approach is to have the inputs into the network being the words in a sentence that surround a given word and have the network try and predict the missing word. We then adjust the weights of the two matrices to minimise the errors that the network makes in these predictions when different bits of text are fed in.
After this training the elements (vectors) of the first matrix have the property that each vector represents a word: a word embedding. Multiplying the matrix by the vector with 15,000 elements representing a given word (having 1 for the element that corresponds to the word) returns the associated vector. This new vector also represents the word but is smaller. It will usually have values in all of its dimensions, rather than in just the one dimension like the vector we started with. The distance between these new vectors, to some extent, corresponds to similarities in the semantic meaning they have e.g. vectors of synonyms should be closer together.
2. The Attention mechanism (enriching how vectors represent relations between words)
Transformers allow us to include more sophisticated information in the ways that vectors represent words. Central to this is a mechanism known as ‘attention’ which is used to enrich words’ vectors with information on the relationship to other words in the text it appears with i.e. it tries to enable the vector that represents a word to include the meaning of the word given the context of the words it appears with. For example in the sentence ‘The dog wagged its tail.’ the word ‘its’ (technically a possessive pronoun) has a special relationship to ‘dog’ and also ‘tail’ in the sentence. However ‘dog’, ‘its’ and ‘tail’ are not connected in sentences in general and so this relationship is not necessarily included in a standard word embedding.
2.1 The value, key and query vectors that are used to calculate attention from the embedding vectors
In the attention mechanism we start with a piece of text with m words
which are mapped into m embedding vectors, one for each word.
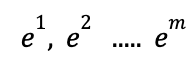
The embeddings can come from pre-existing word embeddings that have already been estimated. Alternatively, a matrix layer before the calculation of attention can be added mapping the vocabulary of words into the dimension of the embedding that is wanted. This is similar to the way a simple embedding is calculated, but with many more layers afterwards.
These embedding vectors are then multiplied by 3 separate weight matrices, to create
three vectors for each word e.g. for the first embedding vector:
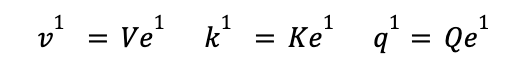
to produce three distinct sets of vectors:
- Value vectors
-
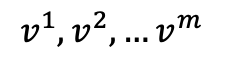
Key vectors
-
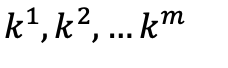
Query vectors

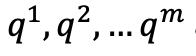
The reason why these three groups of vectors are called key, query and value vectors will become clearer from the description of the attention mechanism in the next section.
The weights in the three matrices are originally created randomly, but are updated during the model training to optimise its ability to predict the next word. The vectors that the embeddings are transformed into are typically of lower dimensionality than the original embedding so the weight matrices have the dimensions of (new_vectors_dimensions x embedding_vectors_dimension). The query and the key vectors need to have the same dimensions to calculate attention, but the value vectors can have a different dimensionality.
Although we are describing the process in terms of three matrices, another approach to implement this, as used in Karpathy’s nanoGPT, is to multiply the embedding vectors by a single larger matrix to produce a longer vector and then split it into query, key and value vectors.
2.2 How attention is calculated for a single word
The attention of a word in a piece of text, such as a sentence, is calculated as a weighted average of the value vectors of all the words in the text (written in the example below as the attention for the first word).
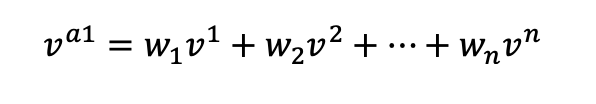
In the original Transformers paper the value vector weights for a word when the attention mechanism is applied
are created by the dot product of the word’s query vector with the corresponding key vectors (for the value vectors) of the
words in the piece of text fed in (including the key and value vectors of the word itself). The resulting numbers are then
divided by a scaling factor: the square root of the dimensionality of the key vector. The mechanism is therefore called
scaled dot product attention. The standard dot product between two
vectors being:
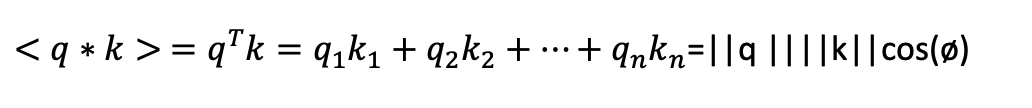If the query vector q is not pointing in a similar direction as the key vector k then the
dot product will be smaller (e.g.
if phi is 90 degrees (pi/2 radians) then cos(phi)=0) and the
vector will be down-weighted in the calculation of attention, while words with more
similar key and query vectors will be given larger weights in the sum of
vectors (e.g. in the dot product of a vector with itself phi=0 and so cos(phi)=1 its maximum value).
The resulting dot products are then divided by the square root of the dimension of the key vector and run through a softmax function to ensure that the weights all sum to one. Dividing by the square root of the dimension of the key vector is done to counteract the fact that, for key vectors with more dimensions, the length of the vectors (The ||v|| terms in the dot product) increases and so the dot product itself goes up. This pushes the softmax function inputs towards larger values which has been found to make models harder to train, so we scale down the values coming from the dot product.
The calculated vector after the attention mechanism is applied is:

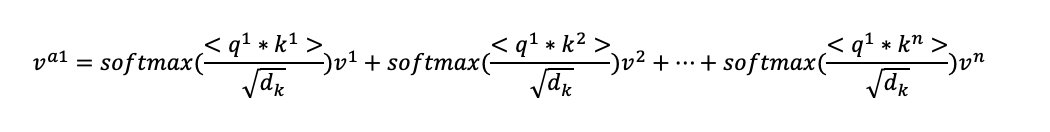
The terms value, key and query vectors come from an analogy with search.
We are searching with a query, values are identified by keys and if a
query is similar to a key the corresponding value is returned. Where the
query and key vectors are less similar, the query is in some sense less similar than the
key, the dot product is smaller and the corresponding value vector is
returned less strongly as it has a lower weight.
In GPTs where a single language is used the same word vector is used to create both key, query and value vectors. In language translation the key and value vectors are created in the source language and attention calculated in combination with the query vectors from the target language.
3. Attention in matrix form (calculating the attention for all the words in a piece of text at one go)
By grouping the three sets of value, key and query vectors into matrices we can form a query matrix (Q), a key matrix (K) and
a values matrix (V), where the rows of these matrices correspond to the query, key and value vectors
respectively. The attention calculation for a piece of text can then be represented by matrix multiplication. Starting with
the multiplication of Q and the transpose of K to get the dot
product used to calculate the weights. This is shown in the simple three word/vector example below:

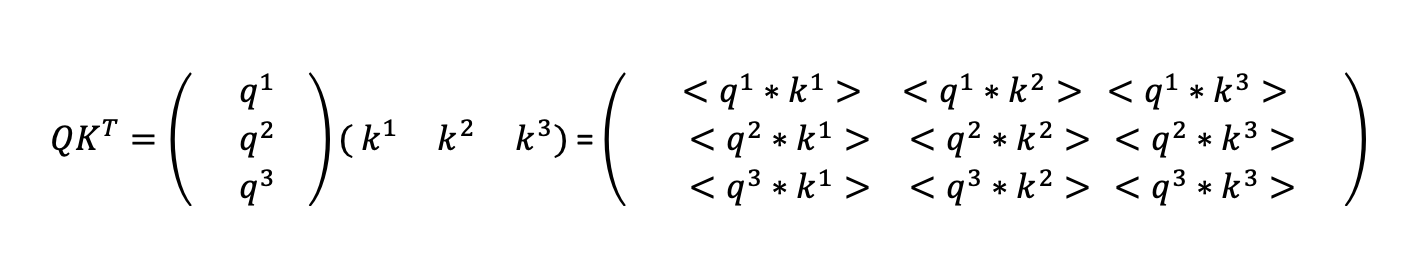
The resulting values are then divided by the square root of the dimensionality of the key
vector and the softmax of the matrix elements taken across the rows. The matrix that this produces is then multiplied by the
values matrix. This is mathematically equivalent to doing the attention calculation for each word
simultaneously.
In the example below we have a values matrix on the right and the calculated weights matrix on the left. Each row of the values matrix corresponds to a different values vector identified by the superscript. The subscript identifies which vector component is involved. The values vectors here have 3 components, but this is just for illustrative purposes; they could have another dimensionality.

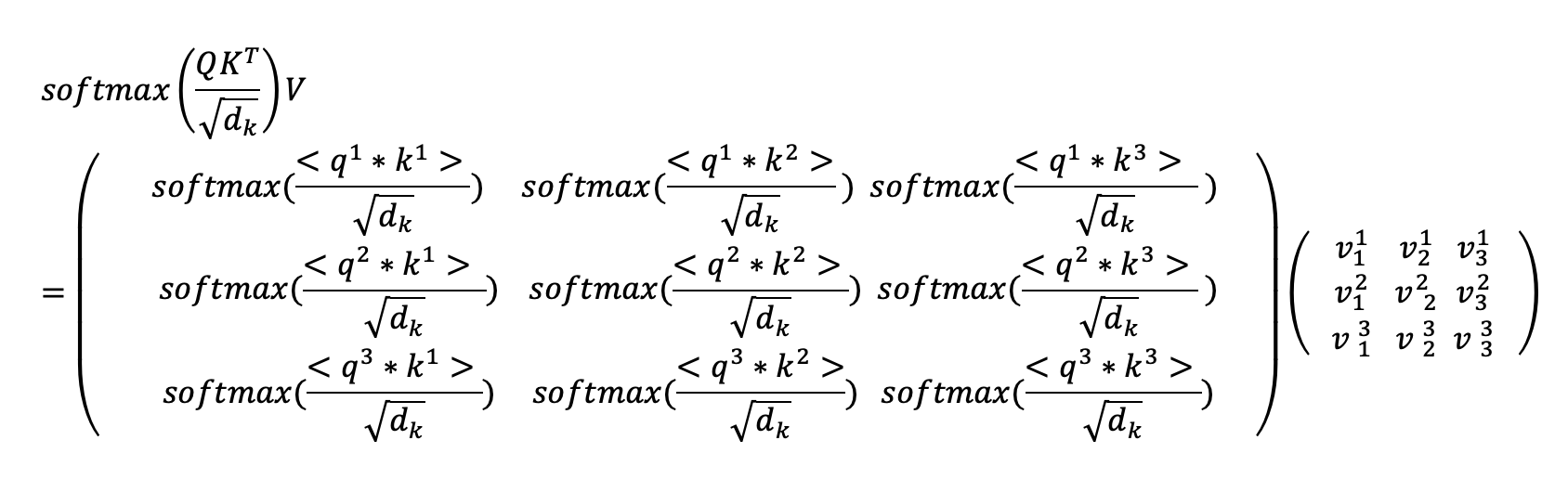
Multiplying out the first row of the weights matrix by the columns of the values matrix and transposing we see that the attention calculation of the first vector is recovered.

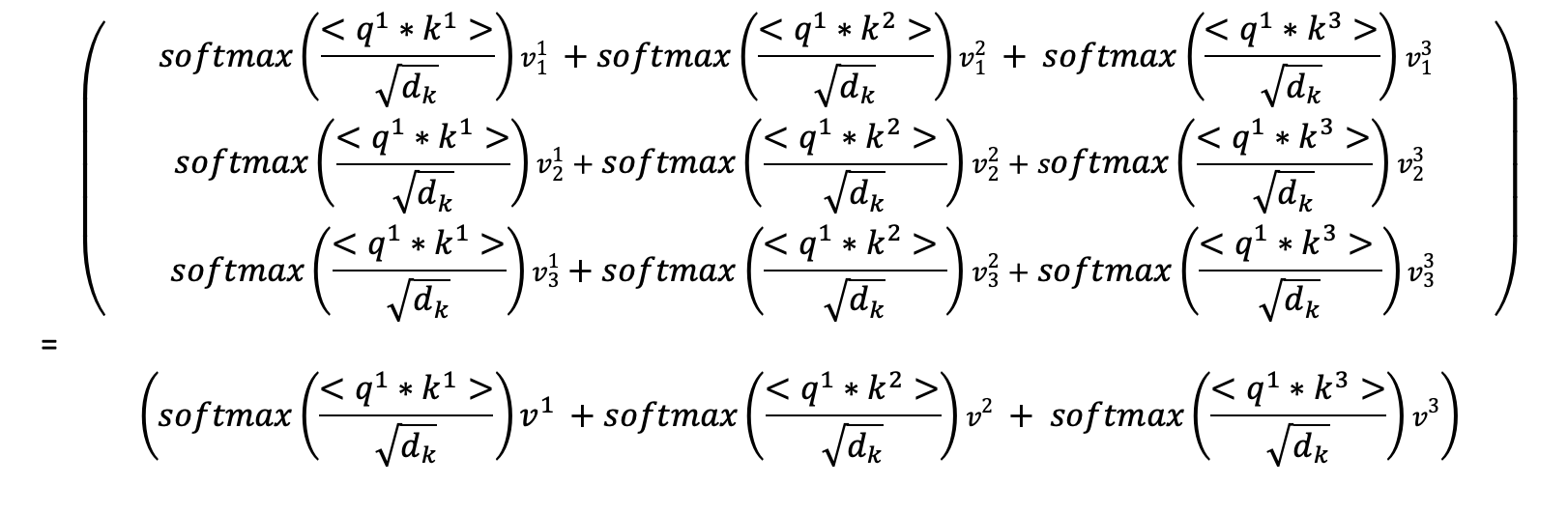
If we multiplied out the second row of the weights matrix we would obtain the attention calculation for the second vector etc. The calculation of attention for all the words in a piece of text can therefore be represented in matrix form:

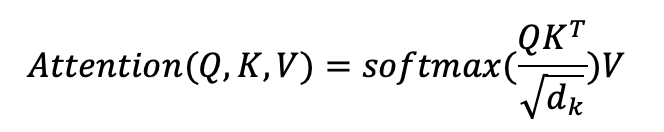
This results in a matrix of dimension (number of words in the piece of text x dimension of the values vector), where each row represents the individual words after the attention mechanism has been applied.
4. Multi-head attention (Encoding multiple relationships between words in a text)
What has just been discussed is a single attention head. The kind of calculation can be done in parallel in a number of independent heads (so called multi-head attention) for the same piece of text. The resulting vectors are then concatenated, to produce one long vector per word which has the dimension of the value vector multiplied by the number of heads.
Each head has separate weights to generate its query, key and value vectors. This enables each head to potentially learn a different representation of the relationships that exist between the words in the text. For example the relationships between nouns and adjectives in a sentence, or between prepositions (e.g. in, and, on, of) and other words etc.
If we had 5 heads and a value vector embedding that is say 200, then when concatenating the vectors produced by the heads we would end up with a vector 1000 elements long for a given word.
To get from the long vector produced by multi-head attention down to one of lower dimension we then multiply this vector by another matrix of weights which has the dimensions of (the models standard embedding dimension x the dimension of multi-head attention). In this example this matrix would have the dimensions of (300 x 1000). These matrix weights are (along with all the other matrix weights) adjusted in training to maximise the network’s performance in predicting the next word from the text that is input into it.
5. How Attention is included in neural networks (and things that have been omitted from the earlier discussion)
We started by generating sets of embedding vectors to represent the collections of words in the pieces of text fed into the network. From each of these embedding vectors we then generated a set of query, key and value vectors. These three vectors are generated separately for however many attention heads we have. In each head we take the query, key and value vectors produced for that head and calculate a new set of vectors for each word using the attention mechanism among the words in a piece of input text. We then stick the vector from each head for a given word together to create one long vector per word in the piece of text. We then multiply by a weights matrix to bring the dimensionality back down to that of the embedding dimension. This results in a new set of vectors representing each word in the text, which have the same dimensions as those we started with, but where the vectors represent the relations between the words better than they did in the original embedding vectors.
We can then start all over again and feed these vectors into a new attention layer and calculate attention again, then take the resulting vectors and calculate it again, and again, and again etc. Calculating multiple layers of attention one after another is considered to be one of the factors behind GPT models' success: GPT3 is reported to have 96 attention layers. Finally, we take the resulting vector outputs from the last layer, multiply it by a matrix of weights to transform the output down to the dimension of the number of distinct words. We then run these numbers through a softmax layer to predict which word is likely to be the next one from the input text. The weights of the matrices in all the layers are then adjusted to optimise the predictions in the data used to train them.
Although this post has discussed how attention is calculated it has omitted some things to keep things simple:
-
How the position of a word in a sentence is captured As described above nothing in the calculation of attention depends on the position of a word in the sentence. In practice an additional vector which represents a word’s position in the sentence is added to the word’s original embedding vector at the beginning to capture this. There are multiple techniques that can generate a vector representing a word’s position.
-
How attention deals with causality As described above attention is calculated between all the words in the input text such as a sentence, but sometimes that is not appropriate. For example if you are trying to get the network to generate a new sentence it should not have direct access in its inputs to the words used to complete a given sentence. The objective is for the network to predict the words to use, not just copy its inputs. To address this attention is often supplemented with filters (called masks) to change which words are included in its calculation.
-
How attention mechanisms are implemented in code and put together to create GPTs or translate from one language to another This post has covered how attention is calculated, but the discussion of attention has been conceptual, rather than how it is calculated in practice and then used to do things. For example there are some further processing stages that are used when the attention mechanism discussed here is included within a neural network e.g. before passing the attention processed vector on to the next layer you add to it the original vector used to create it. There are also details around how exactly these models are trained and used to generate or translate text which have not been discussed.
These are though for another time.
References:
The original Transformers paper ‘Attention is All You Need’, Vaswani et al. (2017)
The repo for Andrej Karpathy’s nanoGPT
Jay Alammar’s ‘The illustrated transformer’
François Chollet’s book ‘Deep Learning with Python (2nd edition)’