Bayes 2: Bayesian inference with Markov Chain Monte Carlo

View from the Peggy Guggenheim Collection, Venice.

In the previous post we calculated the posterior distribution for a parameter we wanted to estimate. However, in practice, this is often not analytically possible and numerical simulations are needed. Here we evaluate the distribution using a Markov Chain Monte Carlo (MCMC) simulation technique.

The idea is to use a Markov chain to generate samples from the distribution we want to evaluate where, as the chain evolves over time, the values it generates have the properties of the posterior’s probability distribution. These techniques have become important in Bayesian inference as they allow complicated probability distributions to be simulated.

This post covers:

1. The Metropolis Hastings MCMC algorithm
2. Why this works
3. Evaluating a Bayesian posterior distribution with MCMC

1. The Metropolis Hastings MCMC algorithm

Here we look at the Metropolis Hastings algorithm. The distribution we want to simulate is labelled as p. We have a state x and from this generate a proposed new state x* with the probability q(x*|x). q is a probability distribution for x* which depends on x, known as a proposal distribution. As the chain evolves over time the distribution of x values it generates has the properties of the distribution p. x is indexed by the time period s: x(s).

The algorithm to simulate the probability distribution is:

Randomly select a starting value of x
Randomly generate a proposed next value for x: x* from the proposal distribution q where the probability of the proposed x* depends on the existing value: x*=q(x*|x)
Compute a probability of accepting the proposal (alpha):
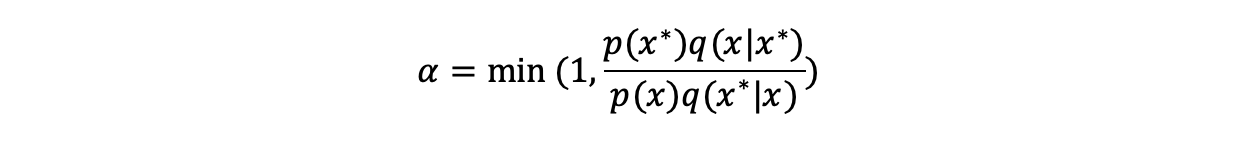The minimum ensures that the probability is not greater than 1
Generate a uniform random number r between 0 and 1
Decide what the next state is according to the rules:
if r < alpha accept the proposal and make the next state x*: x(s+1) = x*
if r >= alpha reject proposal and stick with exiting state: x(s+1) = x(s)
i.e. switch to the new state with probability alpha or stay with the existing state with probability 1-alpha.
Return to 2. and generate a new proposed value from x(s+1)

2. Why this works

That if you run this several thousand times it generates a set of x values that have the probability distribution p(x) is, at least to me, not immediately obvious.

What follows is a plausibility argument taken from Efron and Hastie’s ‘Computer Age Statistical Inference’ that the way the probabilities are constructed means that the distribution of the chain’s states will approach p(x) over time. Here we assume there are a finite number of states M and the probability of state i is labelled p(i). Although the argument is based on a finite number of states in practice a continuous distribution can be approximated by a large number of states.

In a Markov chain there is an equilibrium where for any given state the probability of outflow from the state is equal to the probability of inflow. In this situation the distribution over the states tends to be stable over time as the probability of the state growing or shrinking is the same. We want to show that the equilibrium of the Markov chain we have constructed corresponds to the probability distribution p we want to simulate.

Between two states i and j the probability of switching from state i to state j under the rules Q(i,j) is:
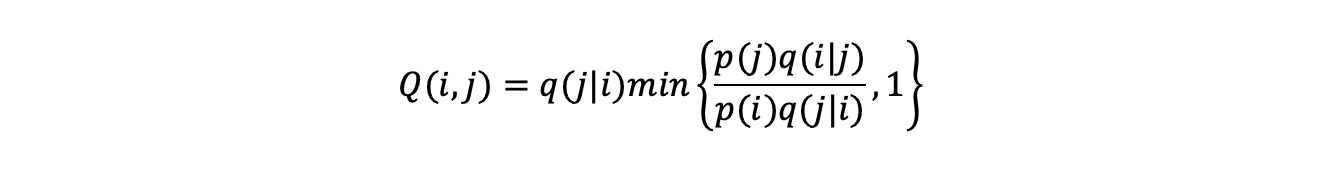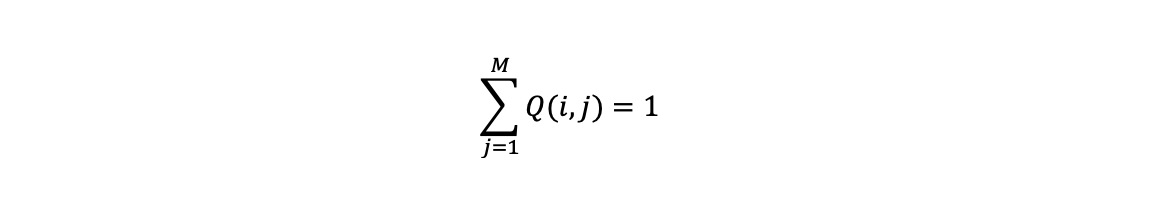
(the probability state j is proposed) x (probability state j is accepted) i.e: mcmc_alg2 These probabilities summed over all possible states that can be reached from i (including staying in state i) sum to 1: mcmc_alg3

The probability of being in state i and then switching to state j is
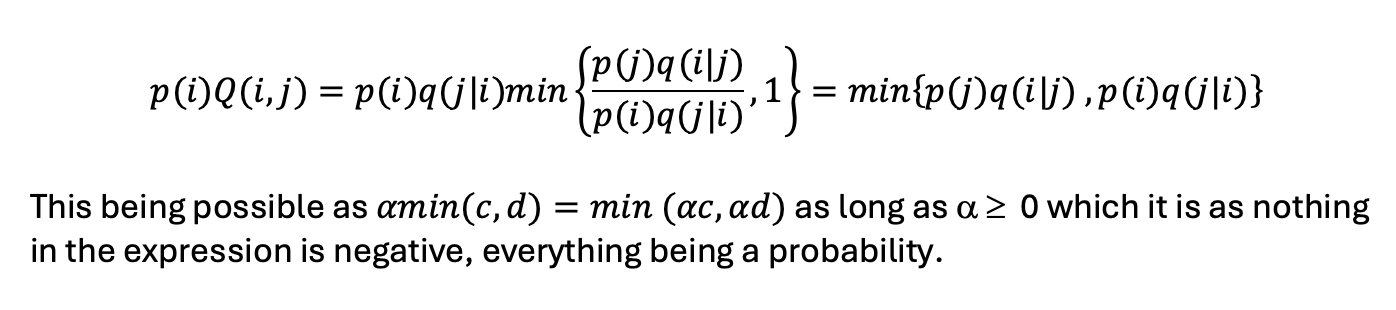
(probability of being in state i) x (probability of switching from state i to j): mcmc_alg4
Similarly, the probability of being in state j and switching to state i is: 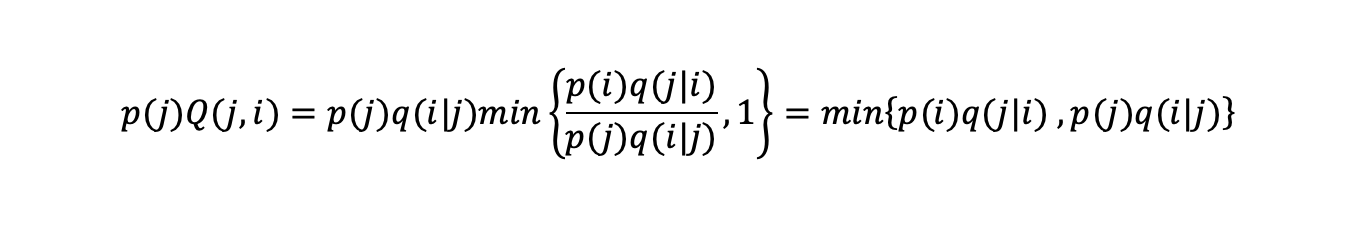mcmc_alg5 min(a,b)=min(b,a) and so the probability of entering state i from state j or vice versa is the same and we have an equilibrium for the probability distribution p(i).
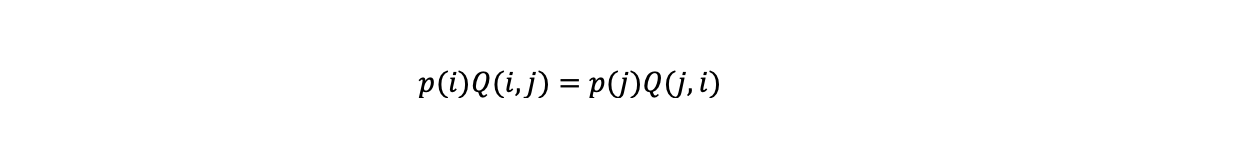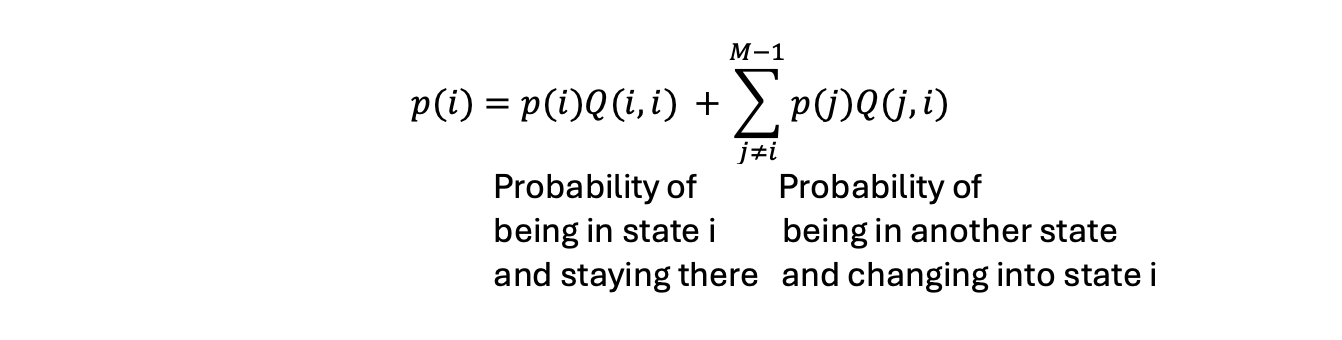mcmc_alg6 Suppose we start in state x(1)=i generated from the probability distribution we want to simulate and calculate the probability of the next state being in state i from one iteration of the chain to the next: mcmc_alg7 Inserting the equilibrium condition and rewriting to look at the second draw from the chain we get: 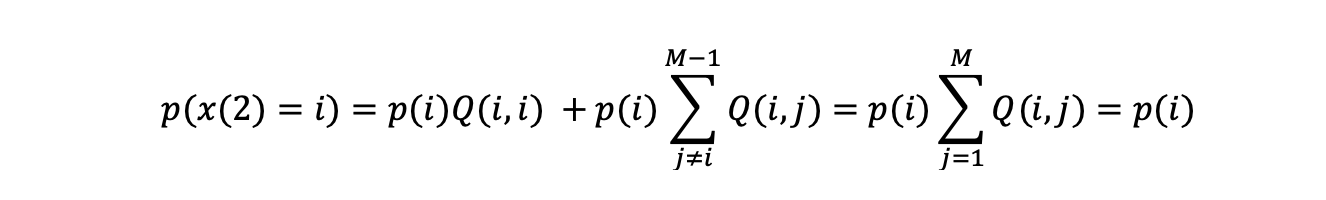mcmc_alg8 The probability distribution of the second draw having state i, has the desired probability p(i), but this equation looks the same for each iteration of the chain so the third, and the fourth draw etc will also have the probability p(i) and similarly for the M-1 other states. p(i) is therefore the equilibrium distribution of the chain. In small samples the chain will not necessarily give the target probability distribution due to random variation, but as we draw more and more the distribution of the chain’s values should approach the probability distribution we want to simulate.

3. Evaluating a Bayesian posterior distribution with MCMC

To see the MCMC algorithm in action we use it to evaluate a simple example: the Gamma posterior produced by the Poisson likelihood and Gamma prior in the last post. This does not need to be simulated as it can be solved analytically, but gives a clear benchmark that we can compare the MCMC simulation against. For other functional forms and complicated situations with many parameters and multi-dimensional priors and likelihoods the posterior’s functional form (or the simpler likelihood multiplied the prior) cannot be directly calculated and therefore the distribution needs to be simulated to evaluate it. Even if you know the posterior distribution, quantities of interest such as its average may not always be readily calculable, but are easy to infer if you have a numerical approximation. The Python code to simulate this and its output are show below.

In the simulation we use a proposal distribution of a Normal distribution with a mean equal to the current state to generate a proposal for the next one. As the lambda which parameterises the posterior can only take positive values, negative proposal values are converted to positive by multiplying by -1.

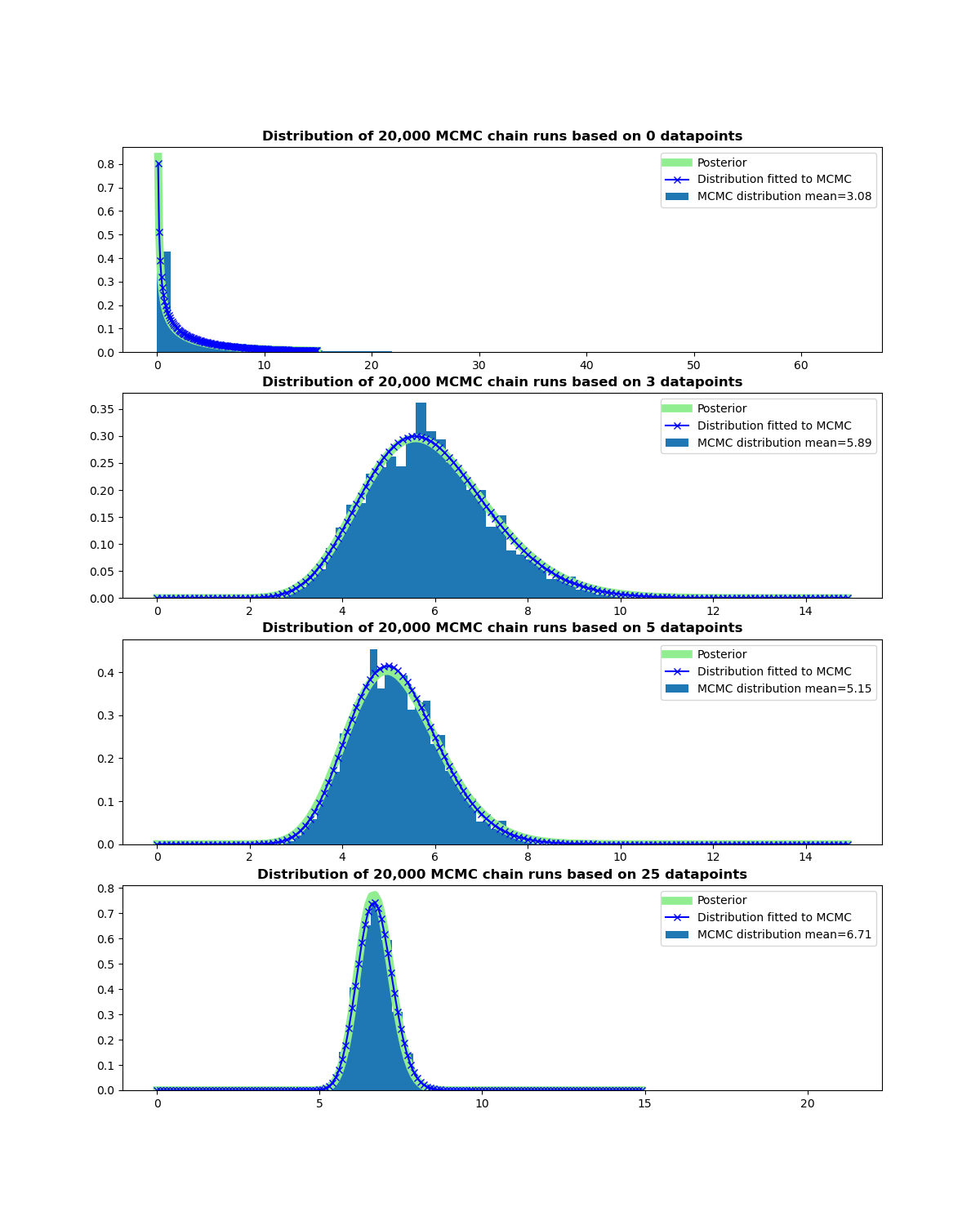
The charts show the posterior for different sample sizes of simulated data used to update the posterior, the corresponding MCMC simulations and the Gamma distribution that corresponds to the MCMC simulation results. The mean and the variance of a Gamma distribution are a function of the parameters alpha and beta that specify it. This relationship can be reversed to estimate these parameters from the mean and variance of the simulations and hence their associated Gamma distributions. 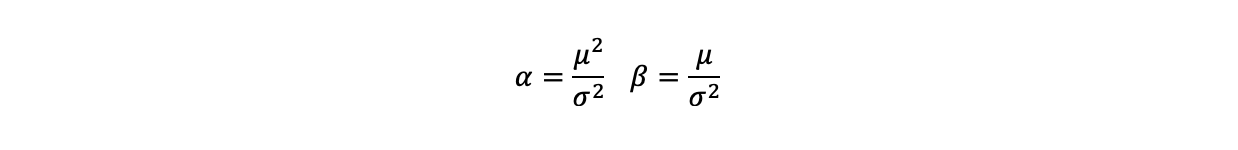mcmc_alg9 As can be seen in the charts the simulated distribution of the chain’s values (and its corresponding Beta function) match the posterior distribution very closely. This is slightly artificial as we know what the true posterior distribution is, but demonstrates that the technique works. In practice things are usually more complicated as the distribution we are trying to simulate will often be unknown and the choice of proposal distribution and random fluctuations in the chain will affect the findings making the assessment of their validity harder.

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy.stats import norm, lognorm
from scipy.special import gamma
from scipy.stats import gamma as gammadist


# Number of samples drawn
sample_number = 20000

# Functions that we are using

def posterior(lambda_val, alpha, beta, data):
    """function that gives the values of the gamma posterior for different values of alpha, beta and data"""

    count_no = len(data)
    sum_val = sum(data)
    new_beta = beta + count_no
    new_alpha = alpha + sum_val

    numerator = (
        (new_beta**new_alpha)
        * np.exp(-lambda_val * new_beta)
        * (lambda_val ** (new_alpha - 1))
    )
    denominator = gamma(new_alpha)

    val = numerator / denominator

    return val


def mcmc_threshold(x, y, data_sample):
    """Function that generates the MCMC probability threshold for accepting the proposed state
    x is the current state
    y is the proposed new state
    norm.pdf(x,y,100) is the function x of a normal distribution with mean y and variance 100
    """
    ratio = (posterior(y, 0.3, 0.1, data_sample) * norm.pdf(x, y, 10)) / (
        posterior(x, 0.3, 0.1, data_sample) * norm.pdf(y, x, 10)
    )

    return min(ratio, 1)

# The sample size of the datasets
data_sets = [0, 3, 5, 25]

# Sets up four subplots and the x axis the data will be evaluated over
fig, axs = plt.subplots(4, figsize=(12, 15))
x = np.arange(0, 15, 0.1)

# For each of the data_sets do a MCMC simulation of the posterior
for index, sample_size in enumerate(data_sets):

    # Create a data frame to hold the results
    data_store = pd.DataFrame(index=range(sample_number), columns=["state_of_chain"])
    # Generate the artifical data to update the likelihood for the different sample sizes
    if index == 0:
        values = []
    else:
        values = list(np.random.poisson(6, sample_size))
    # Create an initial value to start the chain
    initial_value = np.random.normal(10, 10)

    state = initial_value
    

    # Run the samples
    for i in range(0, sample_number):
        # Generate the proposed state
        prop_value = np.random.normal(state, 10)

        # Generate a number between 1 and 0 to simulate probability of acceptance
        prob_sample = np.random.uniform(0, 1)
        
        # Set the proposed value to be positive if it is negative by multiplying by -1
        if prop_value <  0:
           prop_value = -prop_value

        # Condition for accepting or rejecting the proposed state
        if prob_sample < mcmc_threshold(state, prop_value, values):
            state = prop_value
        else:
            state = state
        # Storing the value in the dataframe
        data_store["state_of_chain"].loc[i] = state

    # calculate the mean and the variance of the simulations and from that calculate alpha and beta
    data_mean = data_store["state_of_chain"].mean()

    data_var = data_store["state_of_chain"].var()

    alpha_est = (data_mean**2) / data_var
    beta_est = (data_mean) / data_var


    # chart the distribution of the simulations
    axs[index].hist(
        data_store["state_of_chain"],
        density=True,
        bins=50,
        label=f"mcmc distribution mean={data_mean:.2f}",
    )
    
    axs[index].set_title(
        f"Distribution of {sample_number} MCMC chain runs based on {sample_size} datapoints",
        weight="bold",
    )
    # Plots the posterior distribution we are simulating 
    axs[index].plot(
        x, posterior(x, 0.3, 0.1, values), color="yellow", label="posterior"
    )
    # Calculate the fitted distribution
    axs[index].plot(
        x,
        gammadist.pdf(x, alpha_est, loc=0, scale=1/beta_est),
        color="blue",
        label="fitted distribution to MCMC",
    )
    axs[index].legend()

fig.savefig("mcmc_chart.png")

mcmc_example

References:

Murphy, K. ‘Machine Learning A probabilistic perspective’, Monte Carlo Inference

Donovan, T. and Mickey, R. ‘Bayesian Statistics for Beginners’

Efron, B. and Hastie, T., ‘Computer Age Statistical Inference’

Williams, D., ‘A course in Probability and Statistics’

Bayes 1: Introduction to Bayesian inference

1. The Metropolis Hastings MCMC algorithm#

2. Why this works#

3. Evaluating a Bayesian posterior distribution with MCMC#

Previous posts#

1. The Metropolis Hastings MCMC algorithm

2. Why this works

3. Evaluating a Bayesian posterior distribution with MCMC

Previous posts