View from the Palazzo Leoni Montanari di Vicenza
Crocodile by the Cracking Art collective
Reinforcement learning
In reinforcement learning we have an agent that wants to optimise its outcomes from operating in an environment e.g. a player playing a game, a person consuming and saving, a car driving through a street etc. The agent takes actions which affect the state of the environment and gives it corresponding payoffs. Actions at a given point in time can also affect the future environment, actions and payoffs. We want to work out how to optimise an agent’s outcomes over time given this. Reinforcement learning techniques can help infer what the optimal strategy might be.
To learn more about reinforcement learning I worked through a simple example of this using the game Noughts and Crosses (or Tic-tac-toe as it is called in the US). If this is unfamiliar it is a two-player game where each player takes consecutive turns and places their piece (a Nought or a Cross) on a 3 x 3 grid. The winner is the first to get 3 of their pieces ‘a three’ in a horizontal, vertical or diagonal line. The game has the advantage that it allows many of the standard components of reinforcement learning to be used, while being accessible as it is very simple and not that computationally intensive.
The Python PyTorch framework is used to play the game. The code in what follows is available at the repo here.The general reinforcement learning approach is based on Adam Paszke and Mark Towers' Deep Q Learning tutorial.
We cover this in the following sections:
1. Dynamic programming: Structuring optimisation problems in terms of a value function
2. The game set-up
3. Approximating the game’s value function with a neural network
4. Game play
5. The optimisation problem to estimate the approximate value function
6. Playing the game and training the network
7. The network’s performance at playing the game
1. Dynamic programming: Structuring optimisation problems in terms of a value function
We have an agent choosing a series of actions over time: action_1, action_2,….action_n affecting the environment and leading to a corresponding set of payoffs: reward_1, reward_2, reward_3, etc. We assume that the agent wants to maximise its payoff over time and that some of the actions it can choose will have higher rewards than others. In choosing an action the agent may need to consider that, in addition to a payoff now, that action could affect the environment and payoffs in future. Here where the player starts building its lines of pieces in the game affects future moves and whether it wins.
A central technique in reinforcement learning is dynamic programming. This was developed by Richard Bellman in the 1950s and provides a way to structure optimisation problems by rewriting them in terms of a value function which can make them easier to solve.
1.1 Calculating the value of payoffs over time
The present value to the agent of future rewards can be written as a discounted sum of future rewards. The reward in each period depends on the action (a) chosen in that period and the environment (E). Beta is a discount factor less than 1 weighting payoffs in the future less than the present. We write the present value of future rewards as:
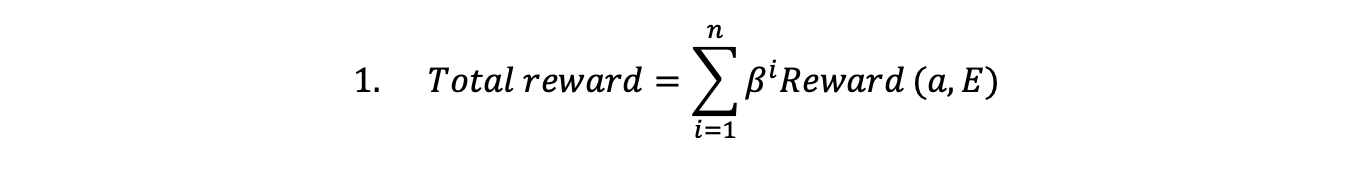 The agent chooses an action from the set of feasible actions in each period to maximise the total reward.
The agent chooses an action from the set of feasible actions in each period to maximise the total reward.
1.2 Writing the value of payoffs over time in terms of a value function
Suppose there is a function the ‘value function’ that summarises what the future implications of a move are. The value function for a given environment state, gives the present value of an action based on the subsequent states that arise, assuming all future actions are chosen optimally to maximise the agent’s payoff.
We can then write the total payoff to a person choosing an action in terms of a value function. The multiple stage optimisation is converted into choosing an action that maximises the reward in the current period and the value function. Here there is no uncertainty and a finite number of future discrete time periods, but versions of what follows can also be applied when these conditions are relaxed.
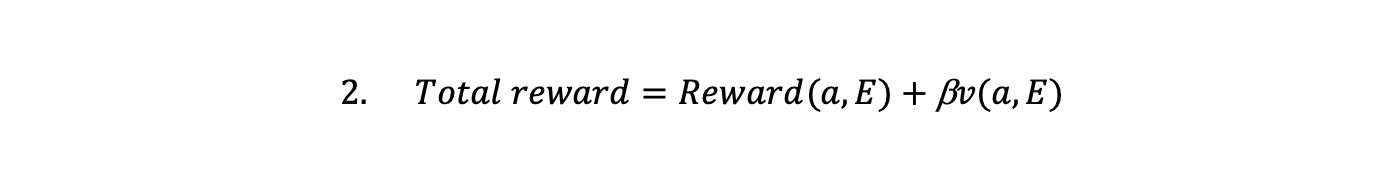
Looking at the total reward rewritten in terms of the value function we can see that the value function is recursive in that, from the
perspective of the present, if we choose the action that maximises the reward + discounted value function then the total reward is itself the value function.
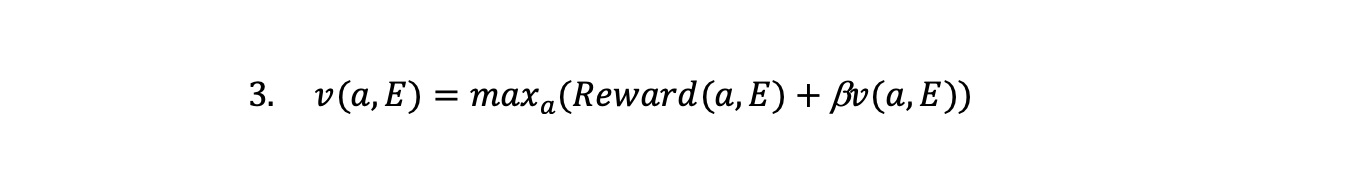 With the value function we have taken a multiple stage decision problem of choosing actions in each time period and changed it into:
With the value function we have taken a multiple stage decision problem of choosing actions in each time period and changed it into:
- Find the value function
- Choose the action in a given time period that maximises the sum of the current payoff and the discounted value function
1.3 Finding the value function
The value function is a function that satisfies the equation above. This provides a strategy to help find it. One way to solve the value function known as Q-learning (Q often being used to denote the value function), is to make a first guess of the value function of v(0)=0 and find the action that maximises the right-hand side of the equation above. This gives us an estimate for v(1) which we substitute for the value function on the right-hand side and solve again for the action that maximises the payoff to give v(2).
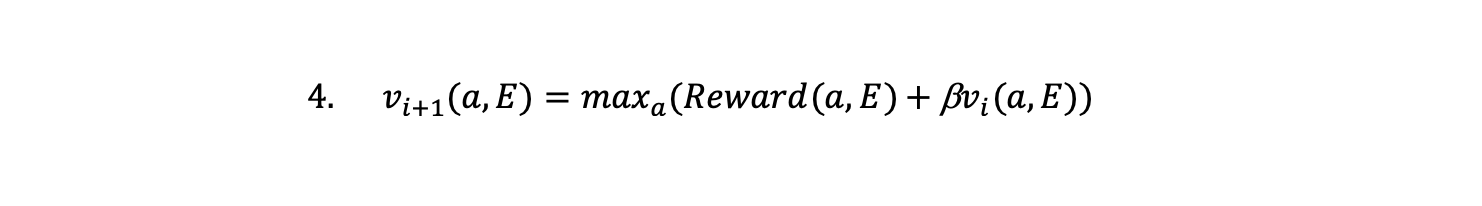
We keep doing this until the function ideally converges to the value function with v(n+1) evaluated for the present state and action being equal to the current reward plus v(n) evaluated at the next state and action that maximises it.
The above is a bit abstract, so let’s implement it with an actual example and some machine learning and see it in action.
2. The game set-up
2.1 The game scripts
The Python code that plays the game is split into:
- config.py holds key parameters
- game.py records the state of the game (the position of pieces on the board) and how the players are doing
- game_moves.py generates the player moves
- game_network.py specifies the network that estimates the value function
- optimising_network.py adjusts the network weights to better satisfy the value function condition
- chart_funcs.py tracks game progress and charts it
- game_learn.py imports all the scripts and runs the training loop that plays the game and trains the network
2.2 The game specification
The game consists of a set of:
- States: The positions of the pieces on the board
- Actions: Placing pieces on the board changing the state
- Rewards: The rewards to the player from the action
Rather than talking about Noughts and Crosses, we will express everything in terms of Player 1 and Player 2. Player 1 plays first followed by Player 2.
In game.py we have two classes:
GameBoard: has the board positions and an update method which changes the positions as a specified player moves its piece. Moves are implemented in terms of Python tuples e.g. the method update((2,2), “player_1”) is when Player 1 places a piece in the bottom right-hand corner. update((0,0), “player_2”) is when Player 2 places a piece in the top left-hand corner.
PersonScore: tracks how many threes, twos and ones scores each player has given the state of the game board.
import numpy as np
import config as config
class GameBoard:
"""Class that keeps track of board positions"""
def __init__(self):
self.board = np.zeros((3, 3))
self.person_1_locs = []
self.person_2_locs = []
self.all_locs = []
def update(self, x, player):
assert (x[0] < 3) and (x[1] < 3)
if player == "player_1":
self.board[x[0], x[1]] = 1
if player == "player_2":
self.board[x[0], x[1]] = 2
self.person_1_locs = list(
zip(np.where(self.board == 1)[0], np.where(self.board == 1)[1])
)
self.person_2_locs = list(
zip(np.where(self.board == 2)[0], np.where(self.board == 2)[1])
)
self.all_locs = self.person_1_locs + self.person_2_locs
class PersonScores:
"""Class that keeps track of the scores of the players"""
def __init__(self, game_board):
self.vertical_scores = list(
zip(
np.count_nonzero(game_board == 1, axis=0),
np.count_nonzero(game_board == 2, axis=0),
)
)
self.horizontal_scores = list(
zip(
np.count_nonzero(game_board == 1, axis=1),
np.count_nonzero(game_board == 2, axis=1),
)
)
self.diagonal_scores1 = [
(
np.count_nonzero(np.diag(game_board) == 1),
np.count_nonzero(np.diag(game_board) == 2),
)
]
self.diagonal_scores2 = [
(
np.count_nonzero(np.diag(np.fliplr(game_board)) == 1),
np.count_nonzero(np.diag(np.fliplr(game_board)) == 2),
)
]
self.all_scores = (
self.vertical_scores
+ self.horizontal_scores
+ self.diagonal_scores1
+ self.diagonal_scores2
)
def assign_rewards(values, config):
"""Function that assigns rewards to the players based on the highest score"""
if 3 in values:
score = config.reward_scores["three_score"]
elif 2 in values:
score = config.reward_scores["two_score"]
elif 1 in values:
score = config.reward_scores["one_score"]
return score
def calculate_rewards(scores_metrics, player):
"""Function that calculates the rewards for the players given a proposed move and the state of the board"""
# Get the scores for player 1 and player 2
player_1_scores = [t[0] for t in scores_metrics]
player_2_scores = [t[1] for t in scores_metrics]
if player == "player_1":
reward = assign_rewards(player_1_scores, config)
if player == "player_2":
reward = assign_rewards(player_2_scores, config)
return reward
def contains_three(tuples):
"""Function that checks if a tuple contains a 3"""
return any(3 in t for t in tuples)
The functions assign_rewards and calculate_rewards take the counts of lines of three, two and single pieces that a player has and calculates the corresponding reward. contains_three is used in the game to see if a line of three pieces has been created and the game won.
2.3 The config file
The config file shown below specifies key parameters for model training and player rewards:
import torch
# The parameters
# The discount factor
GAMMA = 0.9
# The batch size for the replay memory
BATCH_SIZE = 50
# The weight for the soft update of the target network
TAU = 0.05
# The learning rate for the optimizer
LR = 1e-4
# The EPS parameters which specify the transition from random play to using the network
EPS_START = 0.9
EPS_END = 0.05
EPS_DECAY = 1000
# Reward values
reward_scores = {
"three_score": 10000,
"two_score": 2000,
"one_score": 10,
"loss": -5000,
"illegal_move_loss": -6000
}
# Specifies the device to use
device = torch.device(
"cuda"
if torch.cuda.is_available()
else "mps"
if torch.backends.mps.is_available()
else "cpu"
)
The config file contains the rewards for the different game outcomes for Player 1. The highest reward is when Player 1 has a three score and so wins. Fewer pieces in a row (i.e. two or one) lead to lower rewards. If Player 1 loses it gets a negative reward. The most negative Player 1 reward is for losing the game due to an illegal move as playing by the rules and losing is better than losing by breaking the rules.
3. Approximating the game’s value function using a neural network
Under restricted conditions it is possible to prove that the iteration process described in Section 1 will converge to the actual value function. In practice it is only possible to obtain analytical solutions this way in a limited number of situations and one typically needs to compute an approximation to the value function instead.
Here we use a neural network specified in game_network.py to estimate an approximate value function. The neural network’s structure is created by the ValueNet class which takes as its input the state of the board encoded as a 9 dimensional tensor, where each dimension can take integer values 0, 1 and 2. These represent the location of empty spaces and the pieces of players 1 and 2 respectively.
This input passes to an embedding layer of dimensionality 100, which is the reshaped into a single vector concatenating the embedding vectors for each board position. This vector than passes to a series of fully connected layers. In the final layer the values are mapped back to a layer with 9 dimensions representing the value function over the 9 possible moves a player can make.
The network output is aiming to represent the value function for a given move when the environment is in a particular state. We then choose the action corresponding to the network output with the largest value as, if we have the true value function (or something close to it), the move with the highest value should be the move that maximises our payoff. As the network better and better approximates the value function the moves it suggests should provide better game outcomes.
From the first move onwards some of the 9 board locations will represent illegal moves as a player has already placed a piece on them. We do not directly prevent the network from making illegal moves, but penalise it when it plays them by making it lose the game and get the most negative reward payoff so that it learns to avoid them.
import torch
import torch.nn as nn
import torch.nn.functional as F
from config import *
# Define the network
class ValueNet(nn.Module):
def __init__(self):
super(ValueNet, self).__init__()
# Embedding layer: 3 possible values, embedding size 100
self.embedding = nn.Embedding(num_embeddings=3, embedding_dim=100)
# Example first layer after embedding
# Flattening the 3x3 grid (which after embedding will be 3x3x4) to a vector of size 3*3*4 = 36
self.fc1 = nn.Linear(3 * 3 * 100, 75)
self.fc2 = nn.Linear(75, 75) # Fully connected layer
self.fc3 = nn.Linear(75, 9)
def forward(self, x):
# Assuming x is a 3x3 tensor with values 0, 1, or 2
x = self.embedding(x)
x = x.view(-1, 3 * 3 * 100)
x = self.fc1(x)
x = self.fc2(x)
x = self.fc3(x)
return x
# Set up the networks on the device
policy_net = ValueNet().to(device)
target_net = ValueNet().to(device)
def save_checkpoint(model, optimizer, save_path):
"""function to save checkpoints on the model weights, the optimiser state and epoch"""
torch.save(
{
"model_state_dict": model.state_dict(),
"optimizer_state_dict": optimizer.state_dict(),
},
save_path,
)
4. Game play
We train the model to take the role of Player 1. In training we let it switch between two modes of playing:
Mode 1. Completely random play
Mode 2. Play based on choosing a move that maximises the value function we are training
The move behaviour is specified in the file game_moves.py shown below.
In training Player 1 we start with most of its plays being random (effectively exploring the space of moves and seeing what happens as a result). This is done using the function generate_random_tuple. The proportion of times we play using the moves suggested by the network increases as more is learnt about the game. The starting and end proportion of moves played by network and rate of transition between the two are specified by the EPS parameters in the config.py file.
The line below selects the action that maximises the value function for a given state. Policy_net returns values over the 9 possible moves i.e. the index of the optimal move runs 0 to 8. We therefore use the function map_tensor_to_index to map the identified action back to the tuples (x,y) that we use to specify moves on the board in GameBoard.
return map_tensor_to_index(policy_net(state).max(1).indices.view(1, 1))
In addition to updating the class GameBoard, the chosen action is also used to obtain the amount returned by the value function given a particular state. To do this it is mapped from the tuple back into a 9 dimensional tensor using the function create_tensor_with_value_at_index.
Player 2 behaves randomly subject to the restriction that it does not make illegal moves (this is specified by the function select_random_zero_coordinate). Effectively Player 2 represents a stochastic environment that Player 1 is playing against.
import numpy as np
import random
import torch
import logging
import math
from game_network import policy_net, device
import config as config
steps_done = 0
def select_random_zero_coordinate(array):
"""Function that selects a random zero coordinate from a 3x3 array"""
if isinstance(array, torch.Tensor):
array = array.squeeze(0) # Unsqueeze to remove the extra empty dimension
array = array.cpu().numpy()
else:
assert array.shape == (3, 3) # "Input must be a 3x3 array"
zero_coordinates = list(zip(*np.where(array == 0)))
if zero_coordinates:
# return zero_coordinates
return random.choice(zero_coordinates)
else:
return None
def generate_random_tuple():
"""Function that generates a random move represented as a tuple"""
x = random.randint(0, 2)
y = random.randint(0, 2)
return (x, y)
def map_tensor_to_index(tensor):
"""Function that maps the output of the network back to a tuple"""
tensor = tensor.cpu().squeeze(0)
# assert tensor.dim() == 1 and 0 <= tensor.item() <= 8, "Input must be a 1-dimensional tensor with values between 0 and 8"
index = tensor.item()
return index // 3, index % 3
def create_tensor_with_value_at_index(x):
"""Function that maps the tuples corresponding to a move into a 9 dimensional tensor"""
index = x[0] * 3 + x[1]
tensor_action = torch.zeros(9)
tensor_action[index] = 1
return tensor_action
def select_action(state, config):
"""Function that selects an action based on the state. Initially randomly, but later based on the maximum value from policy net"""
global steps_done
sample = random.random()
# The eps threshold for using the network declines over time
eps_threshold = config.EPS_END + (config.EPS_START - config.EPS_END) * math.exp(
-1.0 * steps_done / config.EPS_DECAY
)
steps_done += 1
if sample > eps_threshold:
# play a network move
logging.info("using network")
# tensor = torch.from_numpy(state)
if (state == 0).all():
state = state.to(device)
else:
state = state.long()
# Convert the tensor to long integers
with torch.no_grad():
# pick the action with the larger expected reward.
return map_tensor_to_index(policy_net(state).max(1).indices.view(1, 1))
else: # play a random move
logging.info("using random")
return generate_random_tuple()
5. The optimisation problem to estimate the approximate value function
We want to update the network based on the data so that it approximates the value function as well as possible. To do this we want the function to satisfy the recursive property that equation 3 has.
In training there are two neural networks. A target network (target_net) and a policy network (policy_net).
-
policy_net is used to estimate the value function given the state and the action that the agent took in response (The left side of equation 3).
-
target_net is used to estimate the payoff to the player in the next stage from the present, given the reward in the current stage, the next state and the action that would maximise the payoff (The value function on the right side of equation 3).
If we have a good approximation to the value function then the payoff from policy_net given current state and action should be similar to corresponding reward that person got from its action + the discounted payoff for target_net.
At the start of training both networks have random weights so this will not be true. Given the collected information from the game, we adjust the weights of policy_net to reduce the gap between the two sides of the equation. We then update the target_net weights with the policy_net weights. We then resample the collected data representing game states and payoffs (see discussion below), chose the optimal action again, adjust the policy_net weights again to close the gap and update the target_net weights again. Continuing this process to get a better approximation to the value function and optimal decision making. This is covered in the optimising_network.py script shown below. The script is imported and run by learn_game.py.
import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
import random
from collections import namedtuple, deque
import logging
from config import *
# Importing the network used to play the game
from game_network import policy_net, target_net, device, save_checkpoint
optimizer = optim.AdamW(policy_net.parameters(), lr=LR, amsgrad=True)
# Sets up Transition that will be used to save the previous values
Transition = namedtuple("Transition", ("state", "action", "next_state", "reward"))
class ReplayMemory(object):
def __init__(self, capacity):
self.memory = deque([], maxlen=capacity)
def push(self, *args):
"""Save a transition"""
self.memory.append(Transition(*args))
def sample(self, batch_size):
return random.sample(self.memory, batch_size)
def __len__(self):
return len(self.memory)
# Sets up a list to save the loss scores
loss_scores = []
def optimize_model(memory, BATCH_SIZE, target_net, policy_net, GAMMA, LR):
"""For the batch of returns, actions and values compute an estimated value function and see if it converges"""
if len(memory) < BATCH_SIZE:
logging.info(len(memory))
return
# Sample a batch_size of the memory
transitions = memory.sample(BATCH_SIZE)
# Transpose the batch (see https://stackoverflow.com/a/19343/3343043 for
# detailed explanation). This converts batch-array of Transitions
# to Transition of batch-arrays.
batch = Transition(*zip(*transitions))
# Compute a mask of non-final states and concatenate the batch elements
# (a final state would've been the one after which simulation ended)
non_final_mask = torch.tensor(
tuple(map(lambda s: s is not None, batch.next_state)),
device=device,
dtype=torch.bool,
)
non_final_next_states = torch.cat([s for s in batch.next_state if s is not None])
# Concatenate the batched state, action and rewards
state_batch = torch.cat(batch.state)
action_batch = torch.cat(batch.action)
reward_batch = torch.cat(batch.reward)
non_final_next_states = non_final_next_states.long()
## Compute the estimated value function results (at time t) for the state and corresponding actions in the batch (using policy_net)
# Transfers the action_batch information to the device where state_batch is
action_batch = action_batch.to(state_batch.device).long()
# Identify which action was taken in the batch
action_batch = action_batch.max(1, keepdim=True)[1]
# Get the estimated value function results from policy_net for the state_batch and corresponding action_batch actions
state_action_values = policy_net(state_batch).gather(1, action_batch.long())
## Compute the reward and estimated value function results (at time t+1) using the reward_batch, the next_state and corresponding value function maximising actions (using target_net)
next_state_values = torch.zeros(BATCH_SIZE, device=device)
with torch.no_grad():
next_state_values[non_final_mask] = (
target_net(non_final_next_states).max(1).values
)
next_state_values = next_state_values.unsqueeze(1)
# Add the reward and the discounted next_state_values together to get the expected state_action_values
expected_state_action_values = reward_batch + (next_state_values * GAMMA)
# Compute Huber loss between the next_state_values and the expected_state_action_values
criterion = nn.SmoothL1Loss()
# Seeing how far apart the two state_action_values and the expected_state_action_values are
loss = criterion(state_action_values, expected_state_action_values)
# Append the loss to the loss_scores list
loss_scores.append(loss)
# Optimize the model minimising the loss between the state_action values and the expected state action values
optimizer.zero_grad()
loss.backward()
# In-place gradient clipping
torch.nn.utils.clip_grad_value_(policy_net.parameters(), 100)
optimizer.step()
5.1 The data we collect on move outcomes as the game develops
To train the value function for Player 1, we collect a set of information as the game develops. This information is the:
1. state: state before the player moved
2. action: action the player took in response
3. reward: reward that the player got
4. next_state: next state in the game
If Player 1 wins, loses or draws with its move the reward and next_state can be calculated immediately otherwise they are calculated after Player 2 moves. After we have generated a pre-specified amount of this game play information we use it to estimate the value function. We save this information using the Transition specification and the ReplayMemory class shown below. In each training iteration we randomly the sample for batch_size number of these tuples to be used to evaluate the degree to which the approximate value function satisfies the recursion relationship.
Transition = namedtuple("Transition", ("state", "action", "next_state", "reward"))
class ReplayMemory(object):
def __init__(self, capacity):
self.memory = deque([], maxlen=capacity)
def push(self, *args):
"""Save a transition"""
self.memory.append(Transition(*args))
def sample(self, batch_size):
return random.sample(self.memory, batch_size)
def __len__(self):
return len(self.memory)
5.2 State action values (which is based on policy_net and the current state and action)
The policy_net is used to compute the state_action_values. It takes as its input the states as a batch. Prior to this processing the actions are copied to the device.
action_batch = action_batch.to(state_batch.device).long()
The index of the actions corresponding to the specific action that was taken is extracted across the batch.
action_batch = action_batch.max(1, keepdim=True)[1]
The batch of states is then fed into the policy_net and the corresponding values for the actions chosen are extracted from the network outputs i.e. the network has a 9 dimensional output (one dimension for each action) and we obtain the value corresponding to the action that was chosen:
state_action_values = policy_net(state_batch).gather(1, action_batch.long())
5.3 Expected state action values (which is based on target_net and rewards and the future states)
With the expected_state_action_values we need to get the current reward of a given action and then choose the action, based on the next state, that gives the maximum of our approximate value function target_net.
The next_state and reward values that are input on the right-hand side of equation 3 need to correspond to the values that are on the left-hand side of the equation which is based on the original state and the corresponding action that the agent took in the batch. We then calculate the action which, given next_state maximises the value from target_net and add the corresponding value function maximising value multiplied by the discount factor and the reward that relates to next_state.
We start by processing the batch of next_states to get those where the game is continuing:
non_final_mask = torch.tensor(
tuple(map(lambda s: s is not None, batch.next_state)),
device=device,
dtype=torch.bool,
)
non_final_next_states = torch.cat([s for s in batch.next_state if s is not None])
For states where there is no end state as the game is in play, choose the action that maximises the reward and return the value of the reward. To do this max(1).values extracts the maximum values from the estimated value functions i.e. the payoff from the value function when the optimal action is chosen:
with torch.no_grad():
next_state_values[non_final_mask] = (
target_net(non_final_next_states).max(1).values
)
next_state_values = next_state_values.unsqueeze(1)
From the pre-existing data we have collected we can get the reward information:
reward_batch = torch.cat(batch.reward)
We then put this all together to calculate the expected_state_action_values for the batch.
expected_state_action_values = reward_batch + (next_state_values * GAMMA)
5.4 Updating the loss to minimise the weights
After each training pass the weights of policy_net are updated to reduce the loss metric of the difference between the expected_state_actions_values and the state_action_value.
The loss compares the state_action_values to the expected_state_action_values for a sample of the batch that we have collected.
loss = criterion(state_action_values, expected_state_action_values.unsqueeze(1))
The loss metric is based on SmoothL1Loss() where smaller errors are effectively squared and larger errors are treated in absolute terms making the loss metric less sensitive to outliers. The target_net weights after each training pass are updated as a weighted average of the weights of the policy_net and the target_net.
6. Playing the game and training the network
 Game play, Highbury, September 2024
Game play, Highbury, September 2024
The model game play and training are specified in the learn_game.py script which is the main script that runs all the others. The game play is as follows:
When Player 1 plays there are four possibilities, Player 1:
- plays an illegal move and loses the game
- gets a three after their move and wins
- has played the 9th (and last) move without creating a three and we have a draw
- has neither lost, won or drawn and play passes to Player 2
In all but the last case we calculate the reward for Player 1 after they have played.
When Player 2 plays there are two possibilities, Player 2:
- gets a three after their move and wins (It is impossible for Player 2 to lose immediately due to moving as Player 2’s move cannot produce a three for Player 1)
- does not lose or win and play passes to Player 2
In both cases we calculate the reward for Player 1 after Player 2 has moved. Once we have a state, player_1_action, next_state, reward we convert these into tensors so that they can be used in the optimising process with PyTorch by adding it to the replay memory with:
memory.push(state, player_1_action_tensor, next_state, reward)
The tensor version of player_1_action is relabelled as player_1_action_tensor to distinguish it from the tuple that updates the board and is used to check for illegal moves.
After a Player 1 move and a Player 2 move the function optimize_model() is run to optimise the policy_net weights as discussed in the previous section. The target_net weights are then updated using a weighted average of the policy_net weights and the target_net weights. This form of updating is known as a soft update.
target_net_state_dict[key] = policy_net_state_dict[key] * config.TAU + target_net_state_dict[key] * (1 - config.TAU)
The share of each networks' weights in the updating is given by the parameter TAU specified in the config file.
import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
import logging
import config as config
# Importing the game board and functions to calculate rewards
from game import GameBoard, PersonScores, calculate_rewards, contains_three
# Importing the network used to play the game
from game_network import policy_net, target_net, device, save_checkpoint
# Importing the functions used to create game moves
from game_moves import select_random_zero_coordinate, select_action, create_tensor_with_value_at_index, select_action_model
# Importing the network optimisation functions
from optimising_network import optimize_model, ReplayMemory, loss_scores, optimizer
# Importing charting functions
from chart_funcs import plot_wins, plot_wins_stacked, plot_errors, cumulative_wins
file_handler = logging.FileHandler(
filename="re_learn.log"
)
# Sets up a logger to record the games
logging.basicConfig(
level=logging.INFO,
format="%(asctime)s - %(levelname)s - %(message)s",
datefmt="%Y-%m-%d %H:%M:%S",
handlers=[file_handler],
)
# Sets up the replay memory
memory = ReplayMemory(20000)
# If cuda is available use more games for training
if torch.cuda.is_available() or torch.backends.mps.is_available():
num_games = 5000
else:
num_games = 50
# Sets up a list to register the game outcome which has entries:
# 1. If Player 1 wins, 2. If Player 1 makes an illegal move and loses
# 3. If the game is a draw, 4. If Player 2 wins
game_outcome = []
def main(config):
# Start the training loop
for i_game in range(num_games):
if i_game % 100 == 0:
print(i_game)
# Create a new game
game = GameBoard()
logging.info("Game starts")
for i in range(1, 10):
logging.info(game.board)
if i % 2 != 0:
# Player 1's turn
state = game.board
state = (
torch.tensor(game.board, dtype=torch.int8, device=device)
.unsqueeze(0)
.int()
)
logging.info("Player 1 moves")
# Get the Player 1 action given the state
player_1_action = select_action(state, config)
logging.info(player_1_action)
# Converts the Player 1 action to a tensor so that it can be fed into the network
player_1_action_tensor = torch.tensor(
create_tensor_with_value_at_index(player_1_action),
dtype=torch.int8,
device=device,
).unsqueeze(0)
# If player 1 makes an illegal move end the game
if player_1_action in game.all_locs:
logging.info("Player 1 makes an illegal move")
reward =torch.tensor([config.reward_scores["illegal_move_loss"]],device=device).unsqueeze(0)
logging.info(f" Reward {reward}")
next_state = None
game_outcome.append(2)
memory.push(state, player_1_action_tensor, next_state, reward)
# End the game. There is no next state and the reward is the losing reward
break
else:
# Player 1 makes the move and the game updates
game.update(player_1_action, "player_1")
# If after Player 1 has moved there is a three, Player 1 wins and game ends
if contains_three(PersonScores(game.board).all_scores) == True:
logging.info("Player 1 wins")
# Append a 1 to the game_outcome list indicating a Player 1 win
game_outcome.append(1)
logging.info(game.board)
# Games ends so the next state is the board at the end of the game
next_state = (
torch.tensor(game.board, dtype=torch.int8, device=device)
.unsqueeze(0)
.int()
)
memory.push(state, player_1_action_tensor, next_state, reward)
logging.info("Game ends")
break
# If 9 moves have been played and still no winnr, the game is a draw
elif (
i == 9
and contains_three(PersonScores(game.board).all_scores) == False
):
# Append a 3 to the game_outcone list indicating a draw
game_outcome.append(3)
reward = calculate_rewards(
PersonScores(game.board).all_scores, "player_1"
)
next_state = (
torch.tensor(game.board, dtype=torch.int8, device=device)
.unsqueeze(0)
.int()
)
reward = torch.tensor([reward], device=device).unsqueeze(0)
logging.info(f"Reward {reward}")
memory.push(state, player_1_action_tensor, next_state, reward)
logging.info("Last move - game is drawn")
break
elif i % 2 == 0:
# Player 1 did not win the last move and so it is Player 2's turn
logging.info("Player 2 moves")
# Player chooses a random move
player_2_action = select_random_zero_coordinate(game.board)
# select_action_model(game)
# Update the game's board
game.update(player_2_action, "player_2")
# Convert the board to a tensor to feed it into the network
next_state = (
torch.tensor(game.board, dtype=torch.int8, device=device)
.unsqueeze(0)
.int()
)
# Checks if Player 2 won after the move
if contains_three(PersonScores(game.board).all_scores) == True:
logging.info("Player 2 moves and wins")
# Append a 4 to the game_outcome list indicating a Player 2 win
game_outcome.append(4)
reward = torch.tensor([config.reward_scores["loss"]], device=device).unsqueeze(0)
logging.info(f"Reward {reward}")
logging.info(game.board)
memory.push(state, player_1_action_tensor, next_state, reward)
break
# Player 2 did not win the last move and we calculate Player 1's payoff
elif contains_three(PersonScores(game.board).all_scores) == False:
# Player 1 made a legal move and the game is still in play. This should be the most common scenario
logging.info(
"Player 1 made legal move, player 2 has moved, but not won"
)
reward = calculate_rewards(
PersonScores(game.board).all_scores, "player_1"
)
reward = torch.tensor([reward], device=device).unsqueeze(0)
logging.info(f" Reward {reward}")
memory.push(state, player_1_action_tensor, next_state, reward)
# Perform one step of the optimization (on the policy network) after player 2 moves
optimize_model(memory, config.BATCH_SIZE, target_net, policy_net, config.GAMMA, config.LR)
# Soft update of the target network's weights. New weights are mostly taken from target_net_state_dict
# θ′ ← τ θ + (1 −τ )θ′
target_net_state_dict = target_net.state_dict()
policy_net_state_dict = policy_net.state_dict()
for key in policy_net_state_dict:
target_net_state_dict[key] = policy_net_state_dict[
key
] * config.TAU + target_net_state_dict[key] * (1 - config.TAU)
target_net.load_state_dict(target_net_state_dict)
# Save the model at the end of the training
save_checkpoint(target_net, optimizer, "crosser_trained_new")
# Generate the plot for the number of errors
plot_errors(loss_scores)
# Generate the plot for the number of wins
plot_wins(cumulative_wins(game_outcome))
# Plot a stacked bar chart of how the games are going
plot_wins_stacked(cumulative_wins(game_outcome))
print("Training complete")
if __name__ == "__main__":
main(config)
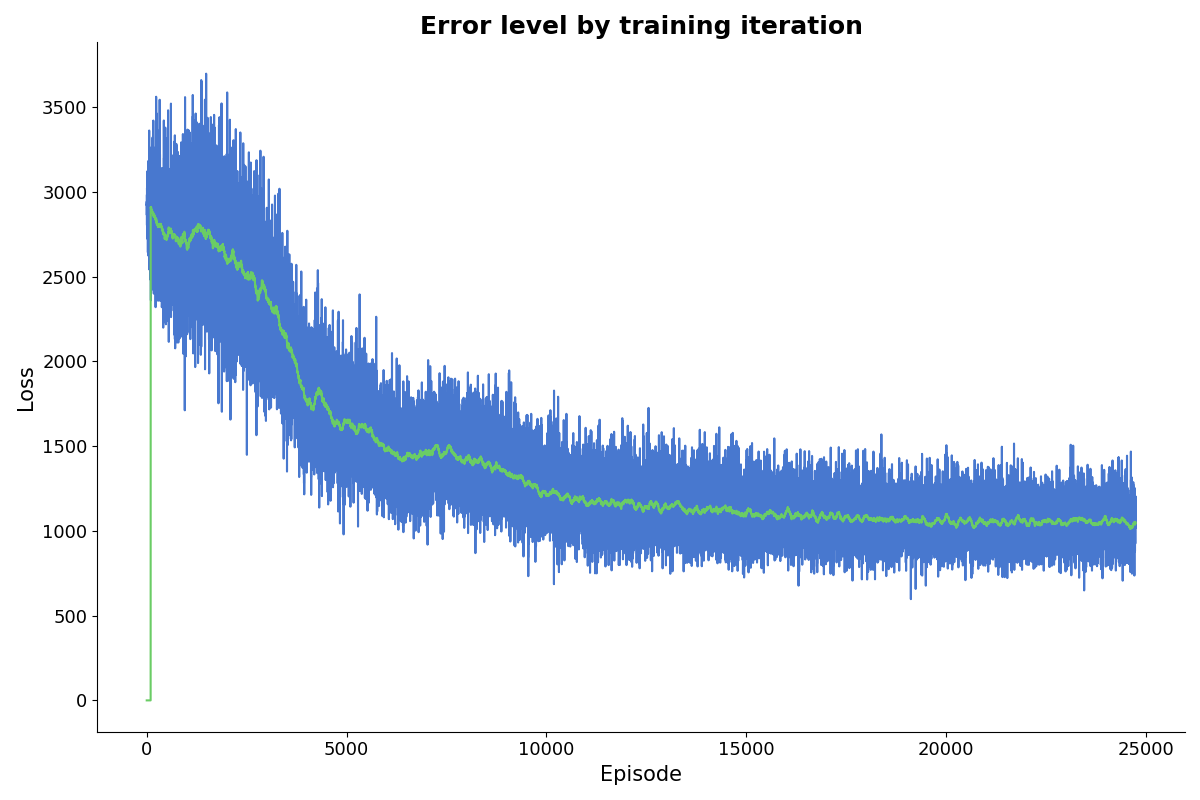
The figure below shows the decline in the gap between the two sides of the value equation as we iterate on it. The charts here and below are generated by chart_funcs.py.
7. The network’s performance at playing the game
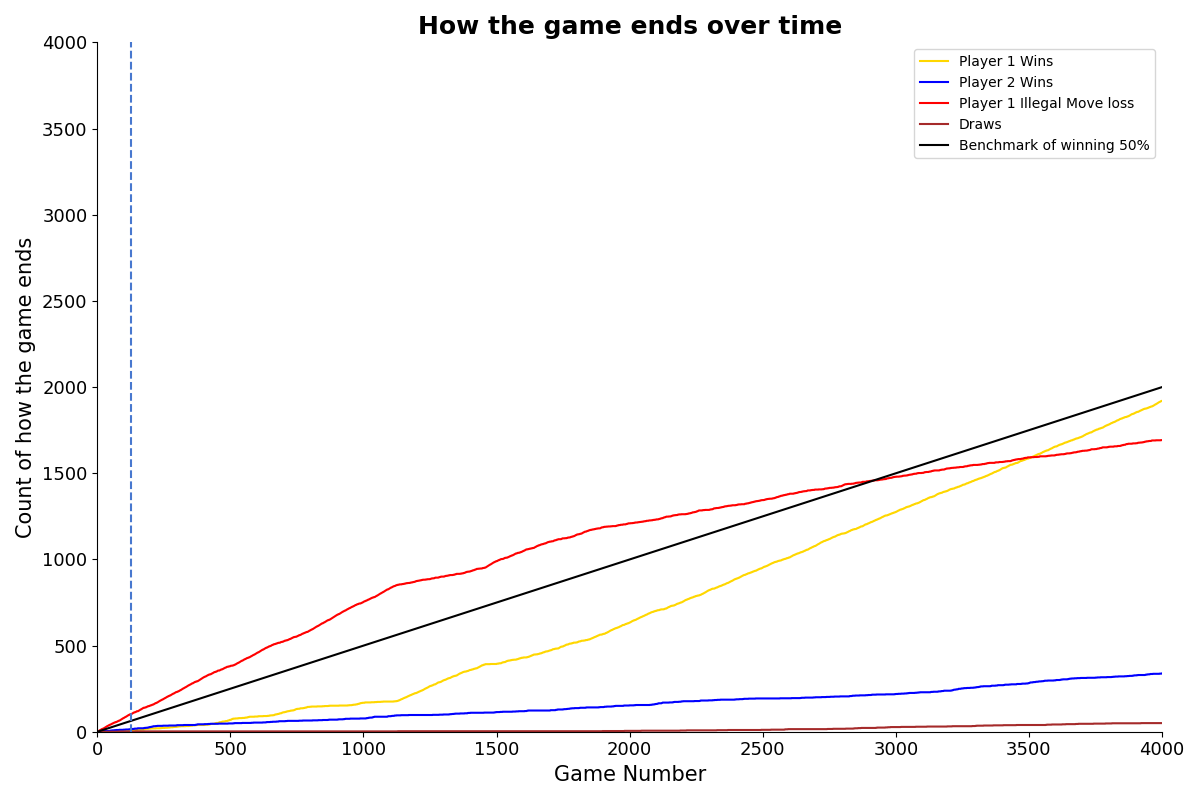
The figure below shows the cumulative number of Player 1 wins, draws and losses (as Player 2 wins or Player 1 makes an illegal move) as the model trains (calculated using the function cumulative_wins() above). Initially as Player 1 plays randomly it makes many illegal moves, gradually though as the network learns it starts to play better and the wins total starts growing faster than the illegal moves total.
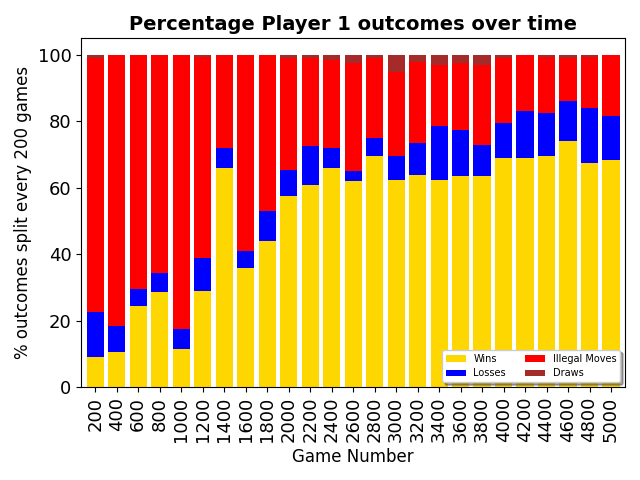
 In the following figure we can see how the share of games that the network is winning rises
as we look at the games in batches of 200. The network does still sometimes make a wrong move, but it has been able to play correctly and win most of the time.
In the following figure we can see how the share of games that the network is winning rises
as we look at the games in batches of 200. The network does still sometimes make a wrong move, but it has been able to play correctly and win most of the time.
 An example game of the network is shown below. This shows that the network as it is facing a random opponent keeps building its line of pieces on the basis that if it gets to two in a row it
probably won’t be stopped in the way that it would be with a normal opponent. As Noughts and Crosses has an optimal strategy that should guarantee a draw, getting the network to converge on that
when it plays itself is an exercise for the future.
An example game of the network is shown below. This shows that the network as it is facing a random opponent keeps building its line of pieces on the basis that if it gets to two in a row it
probably won’t be stopped in the way that it would be with a normal opponent. As Noughts and Crosses has an optimal strategy that should guarantee a draw, getting the network to converge on that
when it plays itself is an exercise for the future.
game begins
[[0. 0. 0.]
[0. 0. 0.]
[0. 0. 0.]]
Player 1 (The network) moves
[[0. 0. 0.]
[0. 0. 0.]
[0. 0. 1.]]
Player 2 moves
[[2. 0. 0.]
[0. 0. 0.]
[0. 0. 1.]]
Player 1 (The network) moves
[[2. 0. 0.]
[0. 0. 0.]
[1. 0. 1.]]
Player 2 moves
[[2. 0. 0.]
[2. 0. 0.]
[1. 0. 1.]]
Player 1 (The network) moves
[[2. 0. 0.]
[2. 0. 0.]
[1. 1. 1.]]
Player 1 (The network) wins
References
Asdam Paszke and Mark Towers, ‘Reinforcement Learning (DQN) Tutorial’ and the repo.
Aurélien Géron, ‘Hands-On Machine Learning with Scikit-Learn, Keras, and TensorFlow’, 2nd Edition
Lars Ljungqvist and Thomas Sargent, ‘Recursive Macroeconomic Theory’
